The Photoelectric Effect
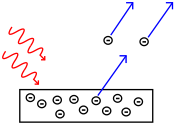
The photoelectric effect is when electrons are emitted from the surface of a metal when light of a certain frequency is directed at it. Electrons are only emitted from the surface of a metal if the light is above a certain frequency, also known as the threshold frequency. Each metal has its own threshold frequency.
The electrons are emitted with a range of different kinetic energies from zero, up to a maximum value. The maximum kinetic energy depends on the frequency of the light, rather than the intensity.
If the light is above the threshold frequency, then the number of electrons emitted per second is proportional to the intensity of light.
The energy needed to remove an electron from the surface of a metal is called its work function, represented by φ. This is usually given in electron volts (eV) and depends on the type of metal.
From formulas, we can deduce that:
Where h is the Planck constant, φ is the work function (J), and E represents the maximum kinetic energy of the electron (J)
Collisions of Electrons with Atoms
When electrons are in their lowest energy orbits, an atom is said to be in its ground state. When a hydrogen atom is in its ground state, its electron cannot lose any more energy. The ground state is the preferred state for an atom, however electrons can move to higher energy levels if the atom absorbs the correct amount of energy. This process is called excitation, and can be caused by the absorption of a photon of radiation of the right wavelength or by a collision with another electron.
Ionisation occurs when an electron gains so much energy until its total energy becomes positive. This means that it becomes free of the atom.
We can show these energy levels in a diagram, where each horizontal line represents the different energy levels.
When an electron falls back to its ground state after becoming excited, a photon with the same amount of energy that was absorbed into the electron during excitation is released.
Excitation in a fluorescent lamp
A fluorescent lamp contains an inert gas, mercury vapour and a light phosphorus coating on the inside of the tube. A high voltage is required in order to produce electrons with a high kinetic energy. These electrons then ionise the mercury ions. The voltage is then lowered, and the flow of electrons through the gas excites the electrons in the mercury atom which later emit UV radiation. The phosphorus coating on the inside of the tube emits visible light when excited with UV, and the whole tube gives off light.
An electron volt (eV) is the amount of energy gained by an electron as it accelerates through a potential difference of a volt.
Energy Levels and Photon Emissions
An electron can only move from one allowed state to another by gaining or losing exactly the right amount of energy. This is called an electron transition. This is why only certain frequencies of light appear in the spectrum.
Each time an electron falls to a lower energy level, it loses energy. This energy is radiated as a photon of frequency f. So the energy of the emitted photon is
Wave Particle Duality
When a bean of light passes through a narrow gap, it spreads out, or it diffracts out. Diffraction can only be explained using waves. If the light was acting as a particle, the light particle in the bean would either not get through the gap, or would pass through and the beam would be unchanged.
The results of photoelectric effect experiments can only be explained by referring to light as a series of particle-like photons. If a photon of light is a discrete bundle of energy, then it can interact with an electron in a one-to-one way. All the energy in one photon is passed to one electron.
As the photoelectric effect and diffraction both display light as both a particle and a wave, we say that light has wave-particle duality.
Louis de Broglie suggested that if "wave-like" light showed particle properties (photons), particles like electrons should be expected to show wave-like properties.
de Broglie came up with an equation that links wavelength (lambda), to the momentum of a moving particle:
where lambda is the wavelength (m), h is planck's constant, m is mass (kg), and v is velocity (m/s)

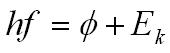




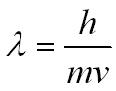
No comments:
Post a Comment