A vector quantity has magnitude and direction, whereas a scalar quantity has magnitude only.
Scalar quantities include: distance, speed, energy, power and mass
Vector quantities include: displacement, velocity, force, acceleration and momentum
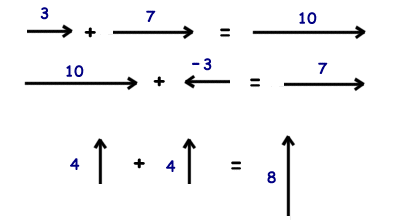
When two vectors are added, we need to take account of their direction as well as their magnitude. Two vectors can be added by drawing a scale diagram by representing each vector as a line, and drawing each vector tip to tail.
The sum of a number of vectors is known as the resultant, The resultant is the single vector that has the same effect as the combination of the other vectors. It is important to take into account which direction the vector is, as the result could change completely.
If we are given two vectors and an angle between them, we are able to easily find the resultant force using trigonometry.
An object is said to be in equilibrium if it is stationary, or moving at constant velocity.
Weight is the force that acts on a mass due to the gravity. It is defined as:
where m represents mass (kg), W is weight (newtons), and g is gravity (N/kg)
An alternative method of investigating these problems is to resolve all the forces into two perpendicular directions, for example horizontal and vertical. If the object is to be in equilibrium, two conditions must be satisfied:
the sum of the horizontal components must equal zero
the sum of the vertical components must equal zero
Moments
The moment of a force about a point is equal to the magnitude of the force, F, multiplied by the perpendicular distance of the force from the pivot, s.
Where f represents force (newtons), and d is distance (m).
The principle of moment states that if an object is in equilibrium the sum of the moments about any point must be zero. Sum of clockwise moments = sum of anticlockwise moments.
Two parallel forces which act in opposite directions will tend to make an object rotate. If these forces are equal in magnitude, they are known as a couple.
The turning effect, or torque, of a couple is Fs, where F is the magnitude of one of the forces and s is the perpendicular distance between the forces.
All the mass of a body can be thought of as acting at a single point, known as the centre of mass of a body. If the resultant force on an object passes through the centre of mass it will accelerate without rotating. If the resultant force does not pass through the centre of mass the object with spin.
Motion Along a Straight Line
Displacement, s, is the distance travelled in a given direction.
Speed is the distance covered in unit time, and can be defined as:
Velocity is a vector quantity. It has a magnitude and a direction. Velocity is the speed in a given direction and is defined as:
where v represents velocity (m/s), d is displacement (m), and t is time (s)
Acceleration is the rate at which velocity changes, and can be defined as:
The gradient of a displacement - time graph is the instantaneous velocity.
A velocity time graph for a journey can be used to calculate the acceleration and the displacement. The gradient of the graph is v/t which is the instantaneous acceleration. A straight line represents constant acceleration. A line with a negative gradient represents a negative acceleration. This could be slowing down or it could mean that the object is speeding up in the opposite direction.
Where s represents displacement (m), u is initial velocity (m/s),v is final velocity (m/s), a is acceleration (m/s^2), t is time (s)
Projectile Motion
An object thrown through the air follows a parabolic path. Even though this is not a straight line, we can still use the equations of motion (SUVAT). This is because horizontal motion does not affect vertical motion.
This means that a two dimensional problem can be solved by treating two one dimensional problems - keeping the horizontal and vertical motions separate.
Newtons Laws of Motion
Newton's First Law of motion states that every object will continue to move with uniform velocity unless it is acted upon by a resultant external force.
Newton's Second Law of motion states that the rate of change of an object's linear momentum is directly proportional to the resultant external force. The change in momentum takes place in the direction of the force.
Where p stands for momentum (kg m/s), m is mass (kg), and v is velocity (m/s)
Where F is force (newtons), m is mass (kg), v is final velocity (m/s^2), u is initial velocity (m/s^2) and t is time (seconds)
Newton's Third Law of motion states that if an object, A, exerts a force on a second object, B, then B exerts an equal and opposite force back on object A.
Work, Energy and Power
The work done is equal to the force multiplied by the distance through which the force moves, in the direction of the force.
Energy is the ability to do work.
Power is the rate at which energy is transferred. A power of 1 watt means that 1 joule of energy is transferred every second.
Power, P, is the rate at which work is done, and can be defined as:
where P is power (watts), W is work done (joules), and t is time (seconds)
For a moving machine, such as a motor or a car, it is often useful to relate the power output to the velocity at which the machine is moving.
We can then deduce that:
Where P is power (joules), F is force (newtons) and v is velocity (m/s)
Conservation of Energy
The principle of conservation of energy states that the total energy of a closed system is constant
The kinetic energy of a moving mass depends on the mass and the velocity squared. We can define kinetic energy as:
W = force x distance = m x g h
This is the same as calculating the potential energy by the mass:
When a mass falls from a height, its potential energy is transferred into kinetic energy. If we can ignore energy losses due to air resistance, then the potential energy will end up as kinetic energy.
During an energy transfer, the total energy stays constant. However, the energy may not all be transferred as useful energy. For example, the engine of a car transfers chemical energy into kinetic energy, however a lot of energy is transferred to thermal energy. The percentage of input energy that is transferred into useful energy is known as it's efficiency.
We can define efficiency as:
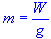
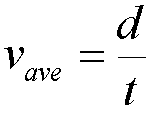
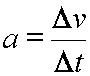
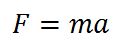
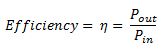
No comments:
Post a Comment