Density is the mass of a given volume, and can be defined as:
When opposing forces are exerted on an object, it becomes stretched or squashed. Tensile forces stretch an object, whereas compressive forces squash an object.
Hooke's Law states that the extension produced by a force in a wire or spring is directly proportional to the force applied and can be defined as:
If we are to test whether a spring obeys Hooke's Law (which it does up to a certain extent), we would set up the experiment as seen below and gradually add more weight to the end of the spring, recording the extension of the spring against the known mass. Should the spring obey Hooke's Law, this would create a straight line on the graph.
Breaking Stress - The maximum amount of stress that can be applied to a material without it breaking.
Brittleness - A brittle material cannot be permanently stretched. When a tensile force is applied the material breaks soon after the elastic limit is reached. Brittle materials may be strong in compression. Widespread use of brittle materials, such as cast iron, concrete and house bricks is only possible if the design keeps them in compression.
Ductility - A ductile material can be easily and permanently stretched. Copper is a good example, and can easily be drawn out into thin wire.
Elasticity - An elastic material returns to its original size and shape when the force which is stretching or compressing it is removed.
Elastic limit - This is the maximum stress that can be applied to a material without causing a permanent deformation.
Hooke's Law - The extension produced by a force in a wire or spring is directly proportional to the force applied. This only applies up to the limit of proportionality.
Plasticity - A plastic material is the opposite of an elastic material. A plastic material does not return to its original size and shape when the force which is stretching or compressing it is removed. There is permanent deformation.
Strength - Some materials can withstand large stresses before they fracture. These are strong or high-strength materials.
Stiffness - This is a measure of how difficult it is to change the size or shape of a material
Tensile Strain - This is the ratio of extension to original length. It is the fractional change in length. It has no unit.
Tensile Stress - This is the force per unit area of cross section when a material is stretched. It is measured in Pascals (Pa)
Yield Point - Beyond the elastic limit, a point is reached at which there is a noticeably larger permanent change in length. This results in plastic behaviour.
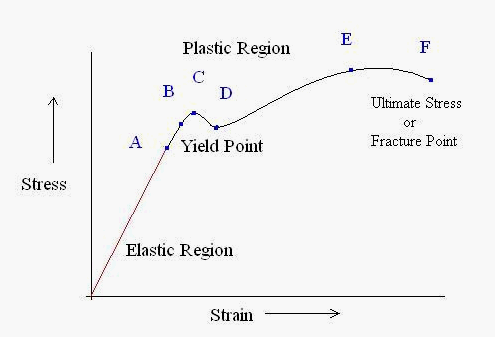
A - This region shows where the object obeys Hooke's Law: extension is proportional to force
B - Proportionality limit - Beyond this point, the extension is no longer proportional to force
C & D- Elastic limit - material begins to behave plastically. This is the point beyond which, when the stress is removed, the material does not return to its original form.
E - Yield point - the material shows large increase in strain for small increase in stress.
F - The material is put under so much stress that it breaks completely
When a wire is stretched by a force, provided the elastic limit is not exceeded, then the work done is stored as elastic strain energy. The area below the graph (in green) is the total work done or the elastic strain energy stored, and can be defined as:
Where E represents the elastic strain energy, F represents the force (N), and delta L is the change in length (m)
We can determine a material's property by looking at their stress/strain graphs and comparing them to other materials eg. brittle against ductile
The Young Modulus
The Young modulus (E) is a measure of stiffness of a material and is defined as:
where F is the force/weight exerted on the wire (N), L is the length of the wire (m) and A is the cross sectional area (m^2)
The Young Modulus can be used to compare the stiffness of different materials, even if the samples have different measurements, however it only applies up to the limit of proportionality.
From a stress-strain graph, we can identify Young's Modulus by:
- calculating the gradient
- multiplying the gradient by length/Area
We can create an experiment in order to determine the Young modulus of a material by setting up as the diagram above. (We can make it more accurate by using two wires instead of one, and using a spirit level in-between them to compare two lengths)
- initially load out the wire to straighten them
- use a micrometer to measure the diameter of the wire
- use a metre rule to measure the initial length of the wire
- slowly add another weight, noting down the total weight on the wire
- use the metre rule to measure out the new length
- calculate the extension
- repeat again until you obtain a varied set of data
- take care and wear eye protection, as the wire may easily snap




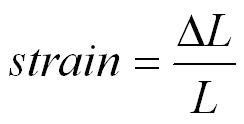


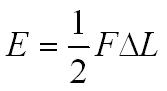


No comments:
Post a Comment